반응형
Skip Connection?
- Skip connections are now a standard module in many convolutional architectures.
- They provide alternative paths for gradients (including backpropagation).
- This additional pathway has been experimentally proven to often help with model convergence.
- In deep architectures, skip connections, as the name suggests, skip some layers of the neural network and provide the output of one layer as input to a later layer instead of the next layer.
- When going backward(back propagation) using the chain rule, we need to keep multiplying the error gradient with terms.
- However, in a long multiplication chain, multiplying many things less than 1 together makes the gradient very small.
- Traditional backpropagation suffers from chain multiplication
- Multiple small terms (<1) lead to vanishing gradients
- Can result in complete gradient death (zero gradients), not updating the early layers at all
- Early layers particularly affected
- Generally, there are two fundamental ways to use skip connections across different non-sequential layers:
- a) Addition, as in Residual architectures
- residual skip connections
- Used in ResNet and variants
- Adds feature maps from different layers
- Preserves dimensionality
- Computationally efficient
- b) Concatenation, as in densely connected architectures.
- Used in DenseNet
- Concatenates feature maps
- Increases feature dimension
- Allows for feature reuse
- a) Addition, as in Residual architectures
ResNet? Skip Connections via Addition
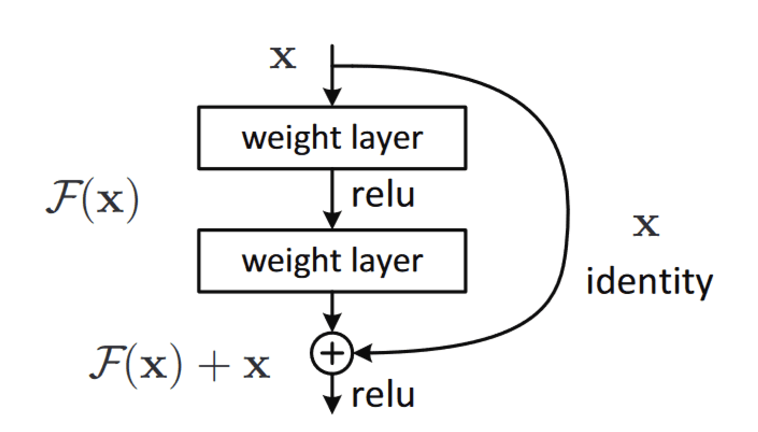
- The core idea is using vector addition to backpropagate through an identity function.
- Then, multiplying the gradient by 1 preserves its value from the previous layers.
- This is the main idea behind ResNets (Residual Networks).
- They stack these skip residual blocks together.
- They use the identity function to preserve gradients.
- Beyond vanishing gradients, there's another commonly used reason.
- For excessive tasks (e.g., semantic segmentation, optical flow estimation, etc.), there is some information captured in early layers that we want to make available for learning in later layers.
- This is because features learned in early layers have been observed to correspond to lower semantic information extracted from the input.
- Without skip connections, the information would have become too abstract.
DenseNet? Skip Connections via Concatenation
- For many dense prediction problems, there is low-level information shared between input and output, and it would be desirable to transmit this information directly through the network.
- Another way to achieve skip connections is to concatenate previous feature maps.
- The most famous deep learning architecture for this is DenseNet.
- This architecture uses extensive feature connections to ensure maximum information flow between layers in the network.
- Unlike ResNet, this is achieved by directly connecting all layers to each other through concatenation.
- In practice, what it basically does is concatenate along the feature channel dimension.
- This leads to:
- a) an enormous amount of feature channels in the last layers of the network
- b) more compact models
- c) extreme feature reusability
Why does Skip Connection results in better performance?
1. Solving the Vanishing Gradient Problem
- Skip connections directly transmit information from shallow layers to deeper layers
- This enables better gradient flow during backpropagation, making effective training possible even in deep networks
- Mathematically, ∂L/∂xl is transmitted with an addition of 1, preventing gradients from becoming too small
- letter l from xl and yl means # layer variable
- Standard network: yl = H(xl)
- Gradient during backpropagation: ∂L/∂xl = (∂L/∂yl) * (∂yl/∂xl)
- As networks get deeper, the ∂yl/∂xl term keeps multiplying, potentially making gradients very small -> Vanishing Gradient
- With skip connection:
- Skip connection: yl = H(xl) + xl
- Gradient during backpropagation: ∂L/∂xl = (∂L/∂yl) * (∂H(xl)/∂xl + 1)
- The addition of +1 term ensures gradients are preserved by at least 1
- Example:
- Standard Neural Network
- ∂L/∂x3 = (∂L/∂y3) * (∂y3/∂x3)
- ∂L/∂x2 = (∂L/∂x3) * (∂x3/∂y2) * (∂y2/∂x2)
- ∂L/∂x1 = (∂L/∂x2) * (∂x2/∂y1) * (∂y1/∂x1)
- With Skip Connection
- ∂L/∂x3 = (∂L/∂y3) * (∂H(x3)/∂x3 + 1)
- ∂L/∂x2 = (∂L/∂x2) * (∂H(x2)/∂x2 + 1)
- ∂L/∂x1 = (∂L/∂x2) * (∂H(x1)/∂x1 + 1)
- Standard Neural Network
- Key Benefits:
- Gradients never become zero due to the added 1
- Stable gradient propagation even in deeper layers
- This enables training of deep networks
- Practical Effects:
- Ability to train deeper networks
- Improved convergence speed
- Better performance achievement
- This is particularly effective when combined with activation functions like ReLU
2. Information Preservation
- Prevents input information from being transformed/lost as it passes through the network
- Important features from shallow layers are well preserved to deeper layers
- Notable is that it enables information transmission through multiple paths
- This allows the network to utilize features at various levels of abstraction simultaneously
3. Optimization Benefits
- With skip connections, instead of directly learning H(x), the network learns F(x) = H(x) - x
- This is an easier form to optimize as the model only needs to learn the residual
- Traditionally, neural networks learned the function H that directly transforms input x into output H(x)
- The goal was to transform the input into a completely new representation
- Instead of learning the entire transformation H(x) directly, the network only needs to learn F(x), which is the residual (difference) from the input
- Residual learning expressed as H(x) = F(x) + x makes it easier to learn transformations close to the identity mapping
- This is particularly important in deep networks, as it allows learning only necessary transformations
4. Ensemble Effect
- Features from various depths are combined to create an implicit ensemble-like effect
- This helps improve the model's generalization performance
- Particularly enables more robust predictions during testing
5. Increased Model Flexibility
- The network can learn how much to utilize skip connections based on the situation
- Can effectively use deep layers when needed and bypass them via skip connections when unnecessary
- The network can automatically adjust its "effective depth"
- During training, if certain layers are deemed unnecessary, their weights can be set close to zero, primarily using the skip connection
6. Benefits in Early Training Stages
- Initial Training Problems in Traditional Deep Learning
- The deeper the network, random initial weights make it difficult to extract meaningful features
- Signals can become distorted or lost as they pass through deep layers
- This results in very slow performance improvement during the early stages of training
- Early Training Advantages of Skip Connections
- Original information from shallow layers is directly transmitted to deeper layers
- This allows the network to begin learning quickly, similar to a shallow network
- The network can gradually learn transformations in deeper layers
- Skip connections help gradient propagation during early training stages
- This plays a crucial role especially in the initial training phases of deep networks
- Helps the network quickly learn meaningful representations during early training stages
Reference
C_4.02 Skip Connections - Backbone
오늘날 딥러닝으로 할 수 있는 응용 프로그램은 무한합니다. 그러나 2014년에 신경망을 훈련시키려고 했다면, 소위 소실 그라디언트(vanishing gradient) 문제에 맞닥…
wikidocs.net
The only limits you have are the limits you place on yourself.
- Max Holloway -
반응형
'캐글' 카테고리의 다른 글
| [Kaggle Study] #5 Statoil/C-CORE Iceberg Classifier Challenge (0) | 2024.11.25 |
|---|---|
| [Kaggle Study] #3 Home Credit Default Risk (1) | 2024.11.24 |
| [Kaggle Study] 16. Translation Invariance (0) | 2024.11.21 |
| [Kaggle Study] 15. Why Use Convolutional Layer? (0) | 2024.11.20 |
| [Kaggle Study] #2 Porto Seguro's Safe Driver Prediction (1) | 2024.11.19 |