Third Competition following Yuhan Lee's kaggle curriculum. Binary classification competition using tabular data.
First Kernel
- General EDA kernel.
Insights/Summary:
1.
This kernel's eda was processed by this order:
- target column(binary var) analysis
- Missing values examination
- data type checking
- unique classes checking for object(categorical) columns
- encoding categorical columns
- anomalies detection
- checking correlations
- ~~~ Feature Engineering ~~~
2.
Missing value examination code sample:
# Function to calculate missing values by column# Funct
def missing_values_table(df):
# Total missing values
mis_val = df.isnull().sum()
# Percentage of missing values
mis_val_percent = 100 * df.isnull().sum() / len(df)
# Make a table with the results
mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)
# Rename the columns
mis_val_table_ren_columns = mis_val_table.rename(
columns = {0 : 'Missing Values', 1 : '% of Total Values'})
# Sort the table by percentage of missing descending
mis_val_table_ren_columns = mis_val_table_ren_columns[
mis_val_table_ren_columns.iloc[:,1] != 0].sort_values(
'% of Total Values', ascending=False).round(1)
# Print some summary information
print ("Your selected dataframe has " + str(df.shape[1]) + " columns.\n"
"There are " + str(mis_val_table_ren_columns.shape[0]) +
" columns that have missing values.")
# Return the dataframe with missing information
return mis_val_table_ren_columns
# Missing values statistics
missing_values = missing_values_table(app_train)
missing_values.head(20)
3.
unique class checking
# Number of unique classes in each object column
app_train.select_dtypes('object').apply(pd.Series.nunique, axis = 0)
4.
Encoding categorical columns: label encoding vs. one-hot encoding
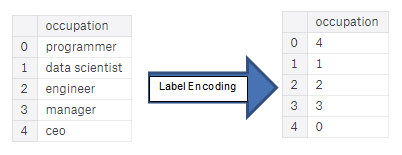
- Label encoding
- Assign each unique category in a categorical variable with an integer
- No new columns are created
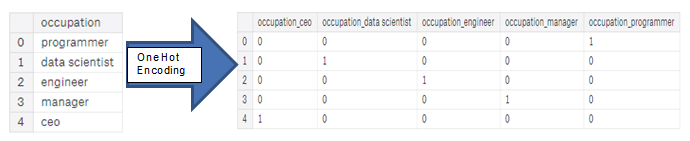
- One-hot encoding
- Create a new column for each unique category in a categorical variable
- Each observation recieves a 1 in the column for its corresponding category and a 0 in all other new columns
- The problem with label encoding is that it gives the categories an arbitrary ordering.
- The value assigned to each of the categories is random and does not reflect any inherent aspect of the category.
- In the example above, programmer recieves a 4 and data scientist a 1, but if we did the same process again, the labels could be reversed or completely different.
- The actual assignment of the integers is arbitrary.
- Therefore, when we perform label encoding, the model might use the relative value of the feature (for example programmer = 4 and data scientist = 1) to assign weights which is not what we want.
- If we only have two unique values for a categorical variable (such as Male/Female), then label encoding is fine, but for more than 2 unique categories, one-hot encoding is the safe option.
- There is some debate about the relative merits of these approaches, and some models can deal with label encoded categorical variables with no issues.
- "I think (and this is just a personal opinion) for categorical variables with many classes, one-hot encoding is the safest approach because it does not impose arbitrary values to categories. The only downside to one-hot encoding is that the number of features (dimensions of the data) can explode with categorical variables with many categories. To deal with this, we can perform one-hot encoding followed by PCA or other dimensionality reduction methods to reduce the number of dimensions (while still trying to preserve information)."
# Create a label encoder object
le = LabelEncoder()
le_count = 0
# Iterate through the columns
for col in app_train:
if app_train[col].dtype == 'object':
# If 2 or fewer unique categories
if len(list(app_train[col].unique())) <= 2:
# Train on the training data
le.fit(app_train[col])
# Transform both training and testing data
app_train[col] = le.transform(app_train[col])
app_test[col] = le.transform(app_test[col])
# Keep track of how many columns were label encoded
le_count += 1
print('%d columns were label encoded.' % le_count)
# one-hot encoding of categorical variables
app_train = pd.get_dummies(app_train)
app_test = pd.get_dummies(app_test)
print('Training Features shape: ', app_train.shape)
print('Testing Features shape: ', app_test.shape)
5.
Anomaly detection
- Handling the anomalies depends on the exact situation, with no set rules.
- One of the safest approaches is just to set the anomalies to a missing value and then have them filled in (using Imputation) before machine learning.
- In this case, since all the anomalies have the exact same value, we want to fill them in with the same value in case all of these loans share something in common.
- The anomalous values seem to have some importance, so we want to tell the machine learning model if we did in fact fill in these values.
- As a solution, we will fill in the anomalous values with not a number (np.nan) and then create a new boolean column indicating whether or not the value was anomalous.
# Create an anomalous flag column
app_train['DAYS_EMPLOYED_ANOM'] = app_train["DAYS_EMPLOYED"] == 365243
# Replace the anomalous values with nan
app_train['DAYS_EMPLOYED'].replace({365243: np.nan}, inplace = True)
app_train['DAYS_EMPLOYED'].plot.hist(title = 'Days Employment Histogram');
plt.xlabel('Days Employment');
6.
Correlation Analysis
- The correlation coefficient is not the greatest method to represent "relevance" of a feature, but it does give us an idea of possible relationships within the data.
- Some general interpretations of the absolute value of the correlation coefficent are:
- .00-.19 “very weak”
- .20-.39 “weak”
- .40-.59 “moderate”
- .60-.79 “strong”
- .80-1.0 “very strong”
# Find correlations with the target and sort
correlations = app_train.corr()['TARGET'].sort_values()
# Display correlations
print('Most Positive Correlations:\n', correlations.tail(15))
print('\nMost Negative Correlations:\n', correlations.head(15))
7.
Making a kernel density estimation plot (KDE) colored by the value of the target:
- A kernel density estimate plot shows the distribution of a single variable and can be thought of as a smoothed histogram.
- It is created by computing a kernel, usually a Gaussian, at each data point and then averaging all the individual kernels to develop a single smooth curve.
- Using the seaborn kdeplot:
plt.figure(figsize = (10, 8))
# KDE plot of loans that were repaid on time
sns.kdeplot(app_train.loc[app_train['TARGET'] == 0, 'DAYS_BIRTH'] / 365, label = 'target == 0')
# KDE plot of loans which were not repaid on time
sns.kdeplot(app_train.loc[app_train['TARGET'] == 1, 'DAYS_BIRTH'] / 365, label = 'target == 1')
# Labeling of plot
plt.xlabel('Age (years)'); plt.ylabel('Density'); plt.title('Distribution of Ages');
8.
Pairs plot
- The Pairs Plot is a great exploration tool because it lets us see relationships between multiple pairs of variables as well as distributions of single variables.
- Here we are using the seaborn visualization library and the PairGrid function to create a Pairs Plot with scatterplots on the upper triangle, histograms on the diagonal, and 2D kernel density plots and correlation coefficients on the lower triangle.
# Copy the data for plotting
plot_data = ext_data.drop(columns = ['DAYS_BIRTH']).copy()
# Add in the age of the client in years
plot_data['YEARS_BIRTH'] = age_data['YEARS_BIRTH']
# Drop na values and limit to first 100000 rows
plot_data = plot_data.dropna().loc[:100000, :]
# Function to calculate correlation coefficient between two columns
def corr_func(x, y, **kwargs):
r = np.corrcoef(x, y)[0][1]
ax = plt.gca()
ax.annotate("r = {:.2f}".format(r),
xy=(.2, .8), xycoords=ax.transAxes,
size = 20)
# Create the pairgrid object
grid = sns.PairGrid(data = plot_data, size = 3, diag_sharey=False,
hue = 'TARGET',
vars = [x for x in list(plot_data.columns) if x != 'TARGET'])
# Upper is a scatter plot
grid.map_upper(plt.scatter, alpha = 0.2)
# Diagonal is a histogram
grid.map_diag(sns.kdeplot)
# Bottom is density plot
grid.map_lower(sns.kdeplot, cmap = plt.cm.OrRd_r);
plt.suptitle('Ext Source and Age Features Pairs Plot', size = 32, y = 1.05);
9.
Kaggle competitions are won by feature engineering: those win are those who can create the most useful features out of the data. (This is true for the most part as the winning models, at least for structured data, all tend to be variants on gradient boosting). This represents one of the patterns in machine learning: feature engineering has a greater return on investment than model building and hyperparameter tuning. This is a great article on the subject). As Andrew Ng is fond of saying: "applied machine learning is basically feature engineering."
While choosing the right model and optimal settings are important, the model can only learn from the data it is given. Making sure this data is as relevant to the task as possible is the job of the data scientist (and maybe some automated tools to help us out).
10.
Feature Construction - Polynomial Features
- One simple feature construction method is called polynomial features.
- In this method, we make features that are powers of existing features as well as interaction terms between existing features.
- For example, we can create variables EXT_SOURCE_1^2 and EXT_SOURCE_2^2 and also variables such as EXT_SOURCE_1 x EXT_SOURCE_2, EXT_SOURCE_1 x EXT_SOURCE_2^2, EXT_SOURCE_1^2 x EXT_SOURCE_2^2, and so on.
- These features that are a combination of multiple individual variables are called interaction terms because they capture the interactions between variables.
- In other words, while two variables by themselves may not have a strong influence on the target, combining them together into a single interaction variable might show a relationship with the target.
- Interaction terms are commonly used in statistical models to capture the effects of multiple variables, but I do not see them used as often in machine learning.
- Nonetheless, we can try out a few to see if they might help our model to predict whether or not a client will repay a loan.
- In the following code, we create polynomial features using the EXT_SOURCE variables and the DAYS_BIRTH variable.
- Scikit-Learn has a useful class called PolynomialFeatures that creates the polynomials and the interaction terms up to a specified degree.
- We can use a degree of 3 to see the results (when we are creating polynomial features, we want to avoid using too high of a degree, both because the number of features scales exponentially with the degree, and because we can run into problems with overfitting).
# Make a new dataframe for polynomial features
poly_features = app_train[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH', 'TARGET']]
poly_features_test = app_test[['EXT_SOURCE_1', 'EXT_SOURCE_2', 'EXT_SOURCE_3', 'DAYS_BIRTH']]
# imputer for handling missing values
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy = 'median')
poly_target = poly_features['TARGET']
poly_features = poly_features.drop(columns = ['TARGET'])
# Need to impute missing values
poly_features = imputer.fit_transform(poly_features)
poly_features_test = imputer.transform(poly_features_test)
from sklearn.preprocessing import PolynomialFeatures
# Create the polynomial object with specified degree
poly_transformer = PolynomialFeatures(degree = 3)
# Train the polynomial features
poly_transformer.fit(poly_features)
# Transform the features
poly_features = poly_transformer.transform(poly_features)
poly_features_test = poly_transformer.transform(poly_features_test)
print('Polynomial Features shape: ', poly_features.shape)Second Kernel
- Kernel about Manual Feature Engineering from the same author with the first kernel.
- Used more data(also provided from the competition) rather than the main train and test data provided from the competition.
- bureau: information about client's previous loans with other financial institutions reported to Home Credit. Each previous loan has its own row.
- bureau_balance: monthly information about the previous loans. Each month has its own row.
- Main idea of the kernel:
- "Manual feature engineering can be a tedious process (which is why we use automated feature engineering with featuretools!) and often relies on domain expertise."
- "Since I have limited domain knowledge of loans and what makes a person likely to default, I will instead concentrate of getting as much info as possible into the final training dataframe."
- "The idea is that the model will then pick up on which features are important rather than us having to decide that."
- "Basically, our approach is to make as many features as possible and then give them all to the model to use!"
- "Later, we can perform feature reduction using the feature importances from the model or other techniques such as PCA."
- Main concept of this kernel was to 1. explain the process of feature engineering 2. show that establishing generalized function can make the process far easier because we can reuse them.
Insights/Summary:
1. Pandas operations
- groupby: group a dataframe by a column. In this case we will group by the unique client, the SK_ID_CURR column
- agg: perform a calculation on the grouped data such as taking the mean of columns. We can either call the function directly (grouped_df.mean()) or use the agg function together with a list of transforms (grouped_df.agg([mean, max, min, sum]))
- merge: match the aggregated statistics to the appropriate client. We need to merge the original training data with the calculated stats on the SK_ID_CURR column which will insert NaN in any cell for which the client does not have the corresponding statistic
- We also use the (rename) function quite a bit specifying the columns to be renamed as a dictionary. This is useful in order to keep track of the new variables we create.
2.
Assessing Usefulness of New Variable with r value
- To determine if the new variable is useful, we can calculate the Pearson Correlation Coefficient (r-value) between this variable and the target.
- This measures the strength of a linear relationship between two variables and ranges from -1 (perfectly negatively linear) to +1 (perfectly positively linear).
- The r-value is not best measure of the "usefulness" of a new variable, but it can give a first approximation of whether a variable will be helpful to a machine learning model.
- The larger the r-value of a variable with respect to the target, the more a change in this variable is likely to affect the value of the target.
- Therefore, we look for the variables with the greatest absolute value r-value relative to the target.
- We can also visually inspect a relationship with the target using the Kernel Density Estimate (KDE) plot.
Kernel Density Estimate Plots
- The kernel density estimate plot shows the distribution of a single variable (think of it as a smoothed histogram).
- To see the difference in distributions dependent on the value of a categorical variable, we can color the distributions differently according to the category.
- For example, we can show the kernel density estimate of the previous_loan_count colored by whether the TARGET = 1 or 0.
- The resulting KDE will show any significant differences in the distribution of the variable between people who did not repay their loan (TARGET == 1) and the people who did (TARGET == 0).
- This can serve as an indicator of whether a variable will be 'relevant' to a machine learning model.
- We will put this plotting functionality in a function to re-use for any variable.
# Plots the disribution of a variable colored by value of the target
def kde_target(var_name, df):
# Calculate the correlation coefficient between the new variable and the target
corr = df['TARGET'].corr(df[var_name])
# Calculate medians for repaid vs not repaid
avg_repaid = df.ix[df['TARGET'] == 0, var_name].median()
avg_not_repaid = df.ix[df['TARGET'] == 1, var_name].median()
plt.figure(figsize = (12, 6))
# Plot the distribution for target == 0 and target == 1
sns.kdeplot(df.ix[df['TARGET'] == 0, var_name], label = 'TARGET == 0')
sns.kdeplot(df.ix[df['TARGET'] == 1, var_name], label = 'TARGET == 1')
# label the plot
plt.xlabel(var_name); plt.ylabel('Density'); plt.title('%s Distribution' % var_name)
plt.legend();
# print out the correlation
print('The correlation between %s and the TARGET is %0.4f' % (var_name, corr))
# Print out average values
print('Median value for loan that was not repaid = %0.4f' % avg_not_repaid)
print('Median value for loan that was repaid = %0.4f' % avg_repaid)
3.
Aggregating Numeric Columns
- To account for the numeric information in the bureau dataframe, we can compute statistics for all the numeric columns.
- To do so, we groupby the client id, agg the grouped dataframe, and merge the result back into the training data.
- The agg function will only calculate the values for the numeric columns where the operation is considered valid.
- We will stick to using 'mean', 'max', 'min', 'sum' but any function can be passed in here.
- We can even write our own function and use it in an agg call.
# Group by the client id, calculate aggregation statistics
bureau_agg = bureau.drop(columns = ['SK_ID_BUREAU']).groupby('SK_ID_CURR', as_index = False).agg(['count', 'mean', 'max', 'min', 'sum']).reset_index()
bureau_agg.head()
# List of column names
columns = ['SK_ID_CURR']
# Iterate through the variables names
for var in bureau_agg.columns.levels[0]:
# Skip the id name
if var != 'SK_ID_CURR':
# Iterate through the stat names
for stat in bureau_agg.columns.levels[1][:-1]:
# Make a new column name for the variable and stat
columns.append('bureau_%s_%s' % (var, stat))
# Assign the list of columns names as the dataframe column names
bureau_agg.columns = columns
bureau_agg.head()
# Merge with the training data
train = train.merge(bureau_agg, on = 'SK_ID_CURR', how = 'left')
train.head()
4.
The Multiple Comparisons Problem
- When we have lots of variables, we expect some of them to be correlated just by pure chance, a problem known as multiple comparisons.
- We can make hundreds of features, and some will turn out to be corelated with the target simply because of random noise in the data.
- Then, when our model trains, it may overfit to these variables because it thinks they have a relationship with the target in the training set, but this does not necessarily generalize to the test set.
- There are many considerations that we have to take into account when making features
Third Kernel
- Stacking Test-Sklearn, XGBoost, CatBoost, LightGBM.
Insights/Summary:
1. Factorizing
# Categorical variables preprocessing
categorical_feats = [f for f in data.columns if data[f].dtype == 'object']
for f_ in categorical_feats:
data[f_], indexer = pd.factorize(data[f_])
test[f_] = indexer.get_indexer(test[f_])- categorical_feats = [f for f in data.columns if data[f].dtype == 'object']
- Find all columns with data type 'object' among all columns in the dataframe
- 'object' type usually represents string or categorical data
- Save the names of these columns in a list
- data[f_], indexer = pd.factorize(data[f_])
- This function encodes categorical data into numbers
- For example, if color data is ['red', 'blue', 'red', 'green'], it will be converted to [0, 1, 0, 2]
- The first return value is the array of encoded numbers
- The second return value (indexer) is the index of the original categorical values
- test[f_] = indexer.get_indexer(test[f_])
- Encode categorical variables in the test dataset using the same method
- Apply the same encoding scheme used in the training data
- This is important to maintain model consistency
2. Stacking Process
1) Use the following 5 different models as Base Models(First-level Models):
xg = XgbWrapper(seed=SEED, params=xgb_params) # XGBoost
et = SklearnWrapper(clf=ExtraTreesClassifier, seed=SEED, params=et_params) # Extra Trees
rf = SklearnWrapper(clf=RandomForestClassifier, seed=SEED, params=rf_params) # Random Forest
cb = CatboostWrapper(clf=CatBoostClassifier, seed=SEED, params=catboost_params) # CatBoost
lg = LightGBMWrapper(clf=LGBMClassifier, seed=SEED, params=lightgbm_params) # LightGBM
2) Generating Predictions through Cross Validation:
# Generate predictions for each model using get_oof() function
xg_oof_train, xg_oof_test = get_oof(xg) # XGBoost predictions
et_oof_train, et_oof_test = get_oof(et) # Extra Trees predictions
rf_oof_train, rf_oof_test = get_oof(rf) # Random Forest predictions
cb_oof_train, cb_oof_test = get_oof(cb) # CatBoost predictions- The get_oof() function uses K-fold cross validation to prevent overfitting while generating predictions
- Generates predictions for both train and test data for each model
3) Creating Meta Features:
# Combine predictions from each model to use as new features
x_train = np.concatenate((xg_oof_train, et_oof_train, rf_oof_train, cb_oof_train), axis=1)
x_test = np.concatenate((xg_oof_test, et_oof_test, rf_oof_test, cb_oof_test), axis=1)- Creates new training data by concatenating predictions from each base model
4) Training Meta Model (Second-level Model):
# Use logistic regression as meta model
logistic_regression = LogisticRegression()
logistic_regression.fit(x_train, y_train)- Trains a final meta model that takes predictions from base models as input
Fourth Kernel
- LightGBM 7th place solution.
Insights/Summary:
1.
Your past does not define your future. You have the power to create your own destiny.
- Max Holloway -
'캐글' 카테고리의 다른 글
| [Kaggle Study] #4 More about Home Credit Default Risk Competition (0) | 2024.11.26 |
|---|---|
| [Kaggle Study] #5 Statoil/C-CORE Iceberg Classifier Challenge (0) | 2024.11.25 |
| [Kaggle Study] 17. ResNet Skip Connection (0) | 2024.11.22 |
| [Kaggle Study] 16. Translation Invariance (0) | 2024.11.21 |
| [Kaggle Study] 15. Why Use Convolutional Layer? (0) | 2024.11.20 |