'오차 역전파'라는 단어를 이해하는 것은 이 분야를 공부하면서 본인을 처음 흠칫하게 한 부분이었다. 나 같은 입문자가 이해하기 위해서는 부가적인 설명이 필요하다고 생각되는 부분이므로 정리하고 넘어가야겠다.
오차 역전파 backpropagation
오차 역전파는 y(타겟 값)와 $ \hat{y} $(예측 값)의 차이를 이용하여 w(가중치)와 b(절편)을 업데이트합니다.
정방향 계산
일단 쉬운 정방향 부터.
'정방향 계산'이란 $ \hat{y} $ 을 구하는 과정을 말한다. 그냥 $ b + \sum_{i=1}^{n}w_{i}x_{i} $ 의 계산이다.
역방향 계산
'역방향 계산'이란 정방향 계산으로 구한 $ \hat{y} $와 $ y $의 오차를 통해 $ w $와 $ b $의 변화율(gradient)를 계산하는 과정이다. 이를 뉴런을 이용한 그림으로 나타내면 아래와 같이 표현할 수 있다.

여기서 책이나 강의를 보면 "오차가 뉴런의 오른쪽 방향에서 왼쪽 방향으로 흐르는 것처럼 보여서 오차 역전파라고 부른다"라고 설명한다. 일단 여기서 글쓴이 본인이 처음 공부할 때 이해가 안 갔던 부분들은:
- 일단 정방향 계산과 역방향 계산이 수행하는 일 자체가 다른데 왜 이름을 '정방향', '역방향'으로 붙였는가
- 가중치와 절편이 오차(변화율)로 인해서 업데이트 된다는 것은 이해가 가지만 "오차가 역전파" 된다는 것이 도대체 무슨 말인가
필자가 이해한 바
일단 여기서 "한 쪽 방향으로 흐른다"는 표현은 필자가 이해하기로는 계산의 "순서"를 의미한다.
다시 말해서, $ w, x, b $의 변수가 $ \hat{y} $가 되는 것이 정방향이라면 역방향은 $ \hat{y} $으로 가중치 w와 절편 b를 업데이트하는 계산을 말하는 것이다. 업데이트하는데에 가장 중요한 역할을 하는 것이 오차이기 때문에 "오차가 역전파"되면서 가중치와 절편을 업데이트시킨다는 말이다.
로지스틱 회귀의 역전파
선형 회귀보다 로지스틱 회귀에서 손실 함수의 미분 과정을 이해하면 '역전파'의 개념을 더 잘 이해할 수 있다.
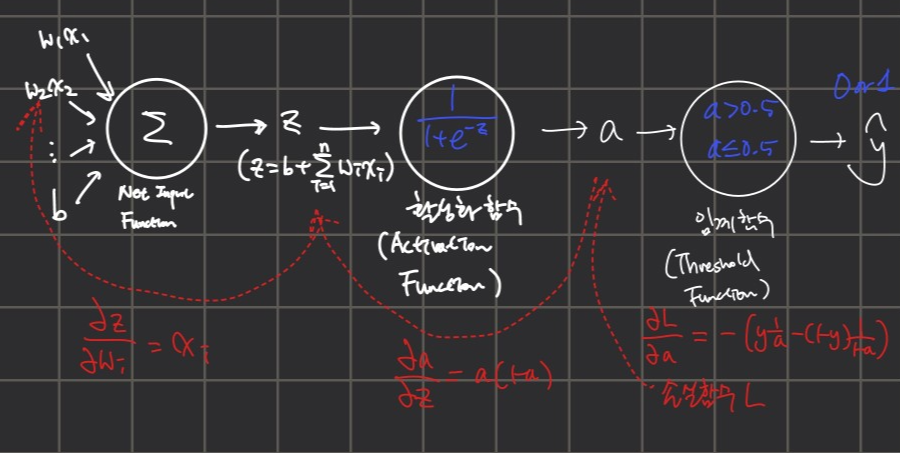
로지스틱 회귀의 손실함수 $ L $은 아래와 같으므로 가중치 $ w $나 절편 $ b $에 대해 바로 미분하면 굉장히 복잡하고 이해하기 어렵기 때문에 연쇄 법칙(Chain Rule)을 이용하여 여러 번의 미분 작업으로 나눠준다. 오른쪽부터 시작해서 1) L을 a에 대해 미분하고, a를 z에 대해 미분하고, z는 w에 대해 미분한다. 각각 미분한 후 결과 값을 곱해서 가중치와 절편을 업데이트하는데에 사용하게 된다.
여기서 로지스틱 손실 함수에 대한 미분이 연쇄적으로 진행되는 모습을 보고 "그레이디언트(변화율)이 역전파된다"라고 말한다.
$$ L = -(ylog(a) + (1 - y)log(1 - a)) $$
따라서 "역전파"가 된다는 것은 정방향 계산을 하며 구했던 값들을 역방향으로 거치며 가중치와 절편을 업데이트하는데에 쓰이는 변화율을 구할 때 사용하는 단어라고 할 수 있다.
혹시 제가 잘못 이해한 부분이 있다면 지적해주세요 :)
할 수가 없었기 때문에 포기한 것이 아니라, 포기했기 때문에 할 수 없었던 것이다.
- 김계란 -
'캐글' 카테고리의 다른 글
| [Kaggle Study] 2. Scale of Features (1) | 2024.10.29 |
|---|---|
| [Kaggle Study] #1 Titanic - Machine Learning from Disaster (2) | 2024.10.26 |
| [Kaggle Study] 1. Loss Function 손실 함수 & Gradient Descent 경사 하강법 (6) | 2024.10.25 |
| ML/DL(3) - 손실 함수와 경사 하강법의 관계 (0) | 2023.07.08 |
| ML/DL(1) - 로지스틱 회귀의 활성화 함수로 비선형 함수를 사용하는 이유 (0) | 2023.07.08 |