로지스틱 회귀는 이름에 '회귀'라는 단어가 들어가서 선형 회귀 등과 비슷한 알고리즘으로 착각할 수 있으나 분류 알고리즘이다.
로지스틱 회귀에 대한 기본적인 내용을 안다는 전제 하에 로지스틱 회귀의 활성화 함수로 비선형 함수를 사용하는 이유에 대해 알아보자.
활성화 함수?
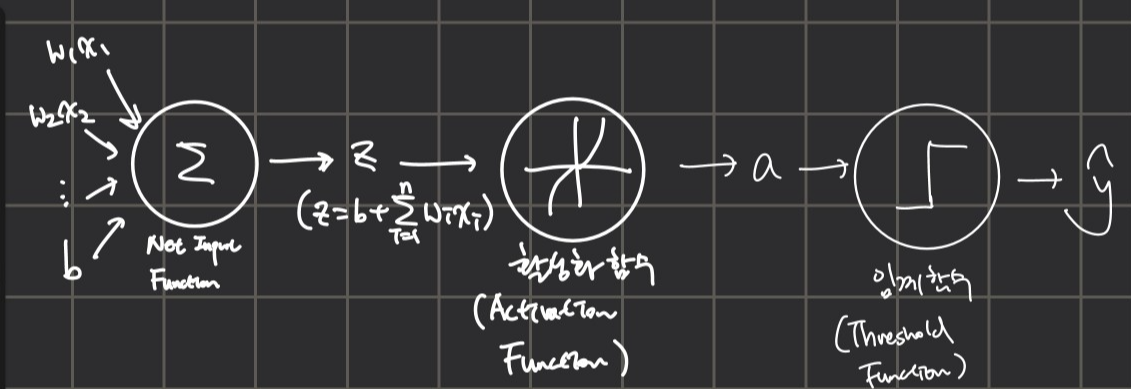
로지스틱 회귀에서는 위의 이미지에서 볼 수 있듯이 선형 함수의 결과로 얻은 결과 값(z)를 변형시켜서 임계함수(threshold function)에 보내게 되는데 이 역할을 수행하는 함수를 활성화 함수(activation function)이라고 한다. 이후 활성화 함수를 통과한 값(a)를 임계함수에 넣어서 예측을 수행한다. 로지스틱 회귀에서 사용하는 활성화 함수는 '시그모이드 함수'로 비선형 함수인데 z 값을 0~1 사이의 값으로 변형시킴으로써 해당 값(a)을 확률로 인지할 수 있게 함과 동시에 1) a > 0.5 2) a <= 0.5 와 같이 두 가지 경우로 나누어 이진 분류를 가능하게 하는 역할을 한다.
여기서 활성화 함수로 선형 함수가 아닌 비선형 함수를 사용하는데에는 이유가 있다.

비선형 함수?
선형 함수란 영어로 번역하면 linear function으로, 말그대로 x와 y 각각의 데이터의 관계가 직선 형태로 나타나게 되는 함수이다. 비선형 함수는 반대로 생각하면 데이터 간의 관계가 직선이 아닌 형태를 띠는 함수이다.
여기서 한 가지 짚고 넘어가야 할 점은 데이터 사이언스는 현실의 데이터를 분석하고 미지의 값을 예측하는 분야로 실제 데이터를 다루게 되는데 현실에서 데이터 간의 관계가 직선 형태로 나타나는 경우는 매우 드물다는 것이다. 이는 비선형 함수를 사용하는 한 가지 이유로 작용한다.
비선형 함수를 사용하는 주된 이유
1) 하나의 층에 하나의 뉴런을 사용한 신경망 알고리즘의 경우
활성화 함수로 선형 함수인 $ y = kz $ 를 사용했다면
$$ z = b + \sum_{i=1}^{n}w_{i}x_{i} $$
에 따라서 $ y = k(w_{1}x_{1} + ... + w_{n}x_{n} + b) $ 가 되므로 이 또한 다시 하나의 선형 함수가 된다.
2) 다층(심층) 신경망일 경우
위의 경우와 유사하게 임계 함수 앞에 뉴런을 여러 개 쌓는 다층(심층) 신경망일 경우에도 활성화 함수가 선형이라면 결국 선형 함수의 결과가 나오기 때문에 별 의미가 없다.
예를 들어, $ y = kz $ 를 $ y = f(z) $ 라고 두면 3개의 층을 쌓는 경우는 $ y = f(f(f(z))) $ 로 표기할 수 있고, 이는 정리하면 $ y = k^{3}z $ 가 되므로 이 또한 선형함수가 된다.
다시 말해, 활성화 함수가 선형 함수일 경우, 여러개의 층을 통과하여 나오는 결과값을 하나의 층을 통과하여 나오는 결과값으로도 해석할 수 있게 되면서 층을 여러 개 쌓는 의미가 없어진다.
결과적으로는 성능이 현저히 떨어진 비효율적인 모델이 된다. 따라서 로지스틱 회귀의 경우뿐만 아니라 거의 대부분의 인공 신경망은 비선형 활성화 함수를 사용한다.
모두가 당신과 누군가를 비교하려고 하고, 당신이 조바심이 나더라도. 천천히, 그리고 오래가십시오. 그게 강한겁니다.
- 김계란-
'캐글' 카테고리의 다른 글
| [Kaggle Study] 2. Scale of Features (1) | 2024.10.29 |
|---|---|
| [Kaggle Study] #1 Titanic - Machine Learning from Disaster (2) | 2024.10.26 |
| [Kaggle Study] 1. Loss Function 손실 함수 & Gradient Descent 경사 하강법 (6) | 2024.10.25 |
| ML/DL(3) - 손실 함수와 경사 하강법의 관계 (0) | 2023.07.08 |
| ML/DL(2) - 오차 역전파(backpropagation) (0) | 2023.07.08 |